1) Calcule:
, onde
e Ω é a região comum entre as esferas:
 |
| Equação (9) |
 |
| Equação (10) |
Primeiro vamos projetar as esferas dadas no plano x = 0, assim como na figura abaixo:
 |
| Figura (1) |
Fazendo isto nossas esferas se transformam em círculos de raio a, e equações:
.gif) |
| Equação (11) |
 |
| Equação (12) |
Agora isolando y na equação (11), e substituindo na equação (12) achamos:
Substituindo este valor de z na equação (11), encontramos:
Agora usando os valores obtidos para z e y para encontrar o ângulo α (veja figura 1), temos:
logo:
Lutamos para encontrar este ângulo, porque ρ é uma constante no intervalo (0, π/3), mas torna-se variável em (π/3, π/2) (observe a figura 1). E como estamos interessados na região comum entre as esferas, primeiro vamos integrar a região que pertence a esfera centrada na origem, e depois integraremos a região da esfera que está centrada em (0, 0, a). Assim se
e de acordo com o sistema de Equações 1 ( que está em:http://legendasdavida.blogspot.com.br/2012/06/coordenadas-esfericas-mudanca-de_22.html):
assim, fazendo a mudança de variáveis, temos:
e
logo, podemos montar a nossa primeira integral:
Observe que nesta integral φ varia no intervalo (0, π/3), e 0 < θ< 2π, 0 < ρ < a, porque dividimos o sólido em duas partes. Assim resolvendo a integral:
Assim encontramos o resultado da nossa primeira integral. Agora vamos ver como se comporta ρ na segunda parte do sólido. Vamos substituir todos os valores referêntes a x, y e a z do sistema de equações 1(veja:http://legendasdavida.blogspot.com.br/2012/06/coordenadas-esfericas-mudanca-de_22.html), na equação 12, e apartir dai encontrar ρ.
 |
| Equação (13) |
substituindo os valores de x, y e z do sistema de equações (1) na equação (13), temos:
Assim, para a segunda parte do sólido:
e assim montamos a segunda integral da mesma forma que a primeira, exceto pelos intervalos onde ρ e φ variam. Agora vamos solucionar a integral:
logo, encontramos o valor da segunda integral. Mas para encontrar o resultado desejado, devemos somar os valores encontrados nas duas integrais, desta forma:
Portanto este é o valor procurado! Valeu galera! até mais!
Observação: Alguma dúvida? Deixe um comentário!
.gif)

.gif)
.gif)
.gif)
.gif)

.gif)





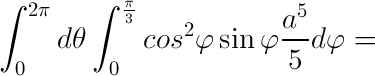


.gif)

.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)


.gif)
Nenhum comentário:
Postar um comentário