Coordenadas Esféricas. Mudança de Variáveis em Integrais Triplas.

Sabemos que não é fácil, encontrar o volume, momento de inércia ou o centro de massa de determinados sólidos usando integrais triplas. Por isso, hoje vamos aprender um método chamado: integrais triplas em coordenadas esféricas, que consiste basicamente em fazer a mudança de coordenadas cartesianas, para coordenadas esféricas em integrais triplas. Esta mudança de variáveis torna a integral mais simples, fato que facilita a integração. Mas, antes de chegarmos onde queremos, vamos dar uma olhada em um teorema muito importante:

O teorema de Fubini, afirma que para resolver uma integral tripla, basta transforma-lá em uma integral iteirada. assim como na equação (2).

Equação (1)

Equação (2)

Onde B é uma caixa retangurar definida por, B = [a, b] x [c, d] x [p, q]. Para resolver a integral iterada na equação (2), fixamos y e z, e integramos em relação a x, em seguida fixamos z, e integramos em relação a y, e por fim, integramos em relação a z.

 Mudando de Variáveis

Para fazer corretamente a mudança de váriáveis em integrais triplas, é nacessário que o leitor obeserve bem o gráfico abaixo:

Gráfico (1)

O ponto (x, y, z) pode ser definido pelas suas coordenadas esféricas (θ, ρ, φ), sabendo que θ é o ângulo entre a projeção de ρ no plano xy e o semi-eixo positivo Ox, e φ é o ângulo entre ρ é o semi-eixo positivo Oz.
Observe que as coordenadas cartesianas do ponto (x, y, z), e suas coordenadas esféricas se relacionam da seguinte forma:

Sistema de Equações

Assim a mudança de variáveis na integral tripla nos dá:

Equação (4)

Equação (5)

, onde sabemos que:

Equação (6)

 e

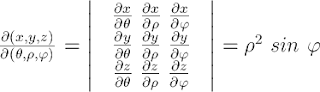Equação (7)

logo:

Equação (8)

A matriz na equação (7) é comumente chamada de matriz jacobiana, seu determinante aparece na equação (5) devido ao teorema de mudança de variáveis na integral tripla. Teorema este que não enunciaremos aqui.

Uma vez terminada a mudança de variáveis na integral tripla, usa-se o teorema de Fubini para integrar.

Observações: (1) A mudança de coordenadas em integrais triplas, ou coordenadas esféricas, é geralmente usada para a integração de sólidos como: esferas, cones ou sólidos semelhantes a estes.

(2) É necessário ter um conhecimento básico sobre cálculo 1, 2, 3 e 4.